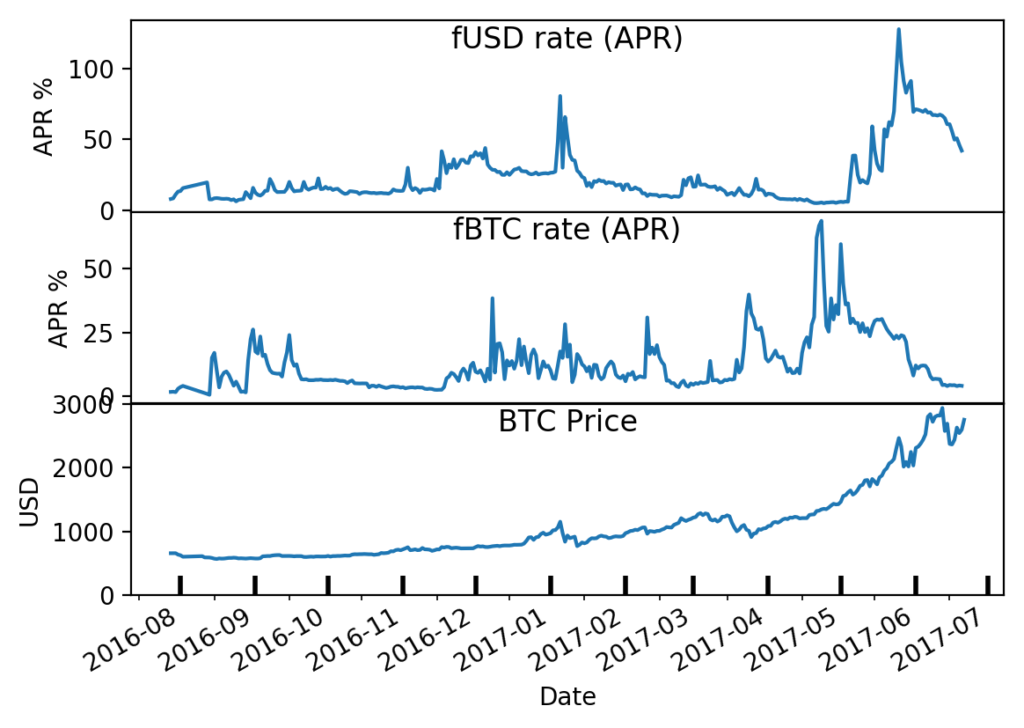
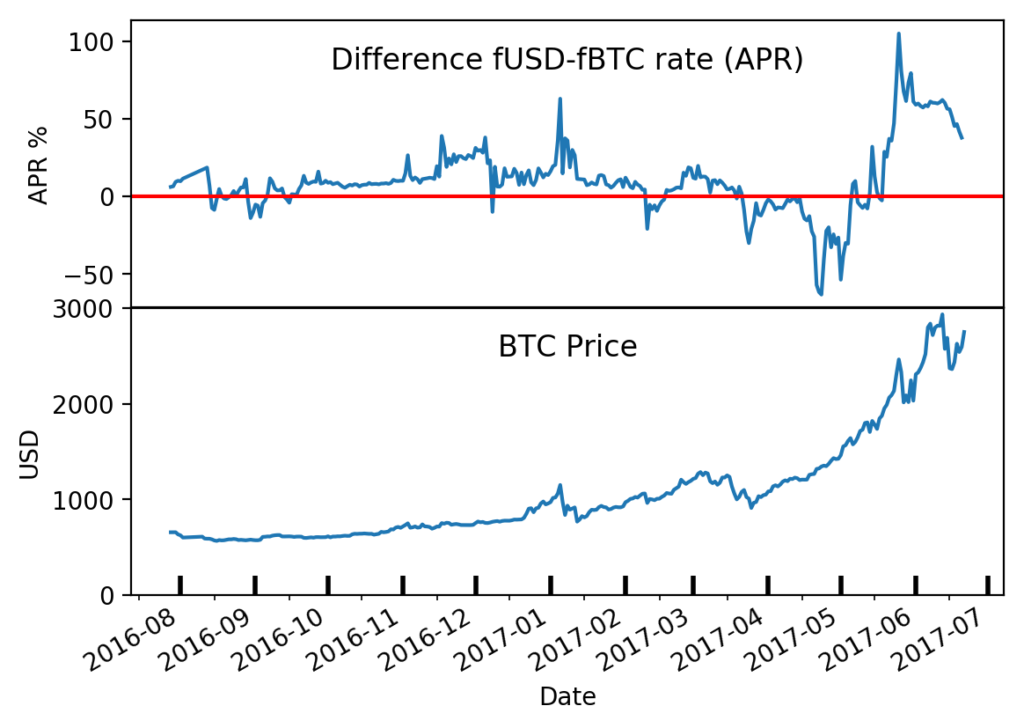
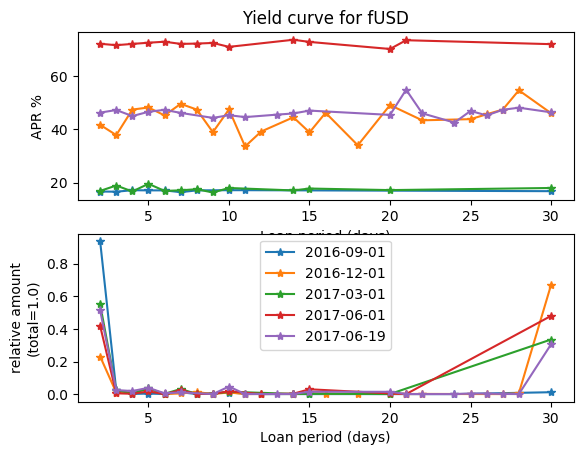
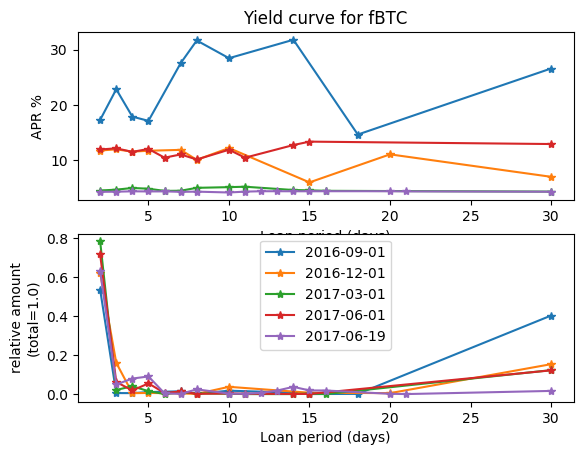
Follow @solverworld Tweet this

The Bitcoin blockchain just split in two.  What is Hash Power and where did it go?  With the split, people are discussing the terms “Hash Power” and trying to decide how many miners are mining each blockchain.  We will present the basic equations for working out these issues, and estimate the relative hash powers mining the 2 chains.

What is the Hash Rate?

Mining is the process by which the bitcoin blockchain is kept secure.  Briefly, the blockchain is a public ledger that everyone “agrees” on that contains the entire history of all bitcoin transaction since time began.  Miners do work (think mining gold) in order to add blocks to the blockchain, for which they get rewarded.  Bitcoin uses what’s called a Proof-of-Work system for mining, other methods used on other cryptos include Proof-of-Stake.

The basic work that the miner has to do is take a batch of current transactions, and find a number, called a nonce, so that the data (in a predetermined format) hashes to a number that is less than a target.

Let’s dissect these pieces one at a time:

1. nonce: named because originally it was a “number used once”, but here it is just a number that the miner is free to pick.  Why the miner would want to pick different ones will be clear shortly.
2. hash: A hash is a function that takes an arbitrary length piece of data and computes a digest, or shorter abbreviation for the data. Note: for the purists out there, we are just considering cryptographic hashes.  Bitcoin uses the hash SHA256, which is a particular hash that produces a 256 bit digest.  The idea of a good hash is that it is very hard to manipulate the data going into the hash to produce any particular hash – effectively it looks like a random number produced from the data (which is always the same for the same data).
3. target: this is a 256 bit number.  Let’s call it T.  It gets calculated a special way on the Bitcoin network, as will be described later.

Now, to rehash things, so to speak:

To successfully add a block to the bitcoin blockchain, the miner must be the first person to find a nonce N, so that:
\[
\textrm{SHA256}(\textrm{SHA256}(\textrm{blockdata}, N)) < T
\]
where blockdata represents the transactions that the miner wants to include in the block. The nonce is in a certain place in that data, but here we call it out as a separate argument to make it clear that the results varies with N. Different miners might want to include different transactions for a variety of reasons, which we don’t need to go into here. Because of the properties of the SHA256 hash, this problem can only be solved (based on our current understanding of SHA256) by repeatedly trying different values of N until we find one that results in our target being hit. The miner has no idea which values of N are better than any others (because the hash is “random”), so they just try them in sequence, 0, 1, 2, 3, … until they find one that gives a hash value less than T. You might ask “why the double hash?”. Excellent question. No one knows for sure, but that’s just the way it is.

How long does it take for a miner to find an acceptable nonce?  Suppose that the miner can calculate H double-hashes per second.  Then, since the result of SHA256 is effectively a random number from 0 to \(2^{256}-1\), the probability of any given attempt satisfying the target is:
\[
prob=\frac{T}{2^{256}}
\]
and the expected time \(E(X)\)to find a new block would be
\[
E(X)=\frac{2^{256}}{T \cdot H}
\]

Difficulty

How is the target T calculated?  The target gets adjusted every 2016 blocks – the idea is that the average time for each block should be 10 minutes.  Thus, if there are so many miners that blocks are found much more frequently, say every 2 minutes, the target T would get adjusted (made smaller), so that the new block times become approximately 10 minutes.
Here are the details of the calculation. It uses something called the Difficulty (D), which is kind of the inverse of the T. That is, the higher difficulty, the lower the target T. You can find the current difficulty from a variety of websites, bitcoinwisdom.com has a nice graph of its history.

Remark: There is something called the packed difficulty (32 bits), which you may see. It is a floating-point representation of the difficulty which is shorter. For example, a packed difficulty 0x1d00ffff becomes:
\[
D_1=\text{0x00ffff} \cdot 2^{8 (\text{0x1d} – 3)}=\text{0xffff}\cdot 2^{208}=\text{0x00000000ffff0000000000000000000000000000000000000000000000000000}
\]
where there should be 52 0’s after the ffff. You can check my counting if you want.
This particular value of difficulty is called difficulty-1, \(D_1\).  It is the highest possible difficulty, and it used to compute the target from the current difficulty D.
\[
T=\frac{D_1}{D}
\]
If the current difficulty were \(D_1\), the target would be 1, and the SHA double hash would have to be 0. With a probability of that happening on each try of \(1/2^{256}\) or \(p=8.636 \cdot 10^{-78}\), that’s pretty hard! The expected number of hashes to find a block for a difficulty D is:
\[
\frac{2^{256}}{T}=\frac{D\cdot 2^{256}}{(2^{16}-1)2^{208}}\approx D\cdot2^{32}
\]
Let X be the time to find a block, we have the following relationships:
\begin{align}
T&=\frac{2^{256}}{D\cdot2^{32}}=\frac{2^{224}}{D}\\
\textrm{E}(X)&=\frac{2^{256}}{T \cdot H}=\frac{D \cdot 2^{32}}{H}
\end{align}
We can reverse the last equation to to estimate the number of hashes per second that a particular time to find a block represents:
\[
\text{hashpower (estimate)}=\frac{D\cdot 2^{32}}{X}
\]
Now, when we see the word “estimate”, we should be thinking “what is its variance?” The estimate here is zero-mean-error, but its variance is quite high. It turns out (I won’t prove it here) that if we expect \(\lambda\) blocks per second, then, for the time per block X:
\begin{align}
\textrm{E}(X)&=\frac{1}{\lambda} \\
\textrm{Var}(X)&=\frac{2}{\lambda^2}
\end{align}
Now, if we average block times over M blocks, the variance can be reduced per the usual formula:
\begin{align}
\textrm{Var}_M(X)&=\frac{2}{\lambda^2 \cdot M} \\
\textrm{std-dev}_M(X)&=\sqrt{\frac{2}{M}}\cdot \textrm{avg}(X)
\end{align}
For an example, the block times for bitcoin are generally around 10 minutes. If we average various numbers of past block times, we get the following standard deviations:

Number of Blocks	Std Deviation of Average Block Time
6	5.77 min
10	4.47 min
20	3.16 min

Thus, we can see that even with looking at the last 20 blocks, we have a great uncertainty in the actual hash power that is operating to produce that block.  Let’s now look at the current block times for Bitcoin and Bitcoin cash and estimate the hash power operating on the chains.  Note that if mining hashpower is switching between Bitcoin and Bitcoin cash, it will take some time to determine that from the data – since we will want more than 20 blocks to average over.

Update 6 Aug 2017 10:47 AM EST:  blocktimes and difficulty dropped significantly (and BTC closer to expected average):

	Bitcoin (BTC)		Bitcoin Cash (BCC)
	Avg Block Time (min)	Std Dev	Avg Block Time (min)	Std Dev
Last 39 (BTC) 20 (BCC) blocks as of 10:47AM EST 6 Aug 2017	9.95	2.25	20.25	6.40
Difficulty	860 221 984 436		144 323 701 657
Estimated Hash Power (double-hash/sec)	6.19 * 10^18		5.1 * 10^17
Relative Hash Power (BTC=1.0)	1.0		.082

 

Note: this is current as of 5 Aug 2017 12:42 AM EST.  I hope to have a online updating version up later.

	Bitcoin (BTC)		Bitcoin Cash (BCC)
	Avg Block Time (min)	Std Dev	Avg Block Time (min)	Std Dev
Last 6 blocks	6.8	3.9	74.3	42.9
Last 20 blocks	6.0	1.9	76.0	24.0
Last 39 (BTC) 29 (BCC) blocks	5.7	1.5	55.6	12.6
Difficulty	860 221 984 436		225 505 642 691
Estimated Hash Power (double-hash/sec)	1.1 * 10^19		2.9 * 10^17
Relative Hash Power (BTC=1.0)	1.0		0.026

References

1. Exponential Distribution
2. Bitcoin Difficulty
3. blockchair.com (for block times)
4. A great detailed discussion of all aspects of bitcoin and other crytpocurrency concepts.
   
5. Discussion geared for a less technical audience